Supraconductivité : Mesure d’une température critique !

Réalisation Margaux Khalil (École Estienne), Julien Bobroff et Frédéric Bouquet (Laboratoire de Physique des solides, Université Paris-Sud et CNRS). Toutes les informations et les autres projets sur opentp.fr

Niveau : Difficile

3 jours

Mesurer la température en dessous de laquelle un matériau devient supraconducteur

Principe physique

La supraconductivité est un phénomène suprenant se manifestant en dessous d’une température, dite température critique .
Environ

\[ T_c = 100K = -173°C \]

pour les meilleurs HTSC (high-temperature superconductor).
En dessous de cette température, les interactions du monde quantique se manifestent à notre échelle. Tout comme la condensation de Bose-Einstein, un objet macroscopique expose alors des propriétés inenvisageables avec une théorie classique.
En particulier, les électrons de conduction d’un solide supra ne se comportent plus de la même manière, on a une chute de résistivité.
La supraconductivité à haute température reste toutefois loin d’être totalement comprise par les physiciens et reste un domaine de recherche très actif en vue des incroyables applications possibles.

On vous propose de mesurer la résistance d’un supraconducteur en fonction de sa température, pour exposer le changement de régime à la température critique , c’est a dire tracer \( R = f(T) \)

Résistances
Résistance platine
Arduino
Fils électriques
Bac de glace
Azote liquide
Fer à souder
Platine d'expérimentation
Résistance supra ( cuprate Tc~100K )
Amplificateur de tension

Matériel

De quoi isoler thermiquement le système : papier aluminium , polystyrène….

Une part importante du tutoriel consiste en la préparation d’appareils de mesure adaptés. Si vous avez déjà à votre disposition un milliohmmètre et un thermomètre pouvant fonctionner à très basse température, le principe de la mesure reste simple : résistance en fonction de la température /\( R = f(T) \) .
L’aquisition peut être gérée par une puce arduino qui s’effectuera en mesure de tension.

Mesure de résistance, les doigts dans l'nez !

Monter la résistance sur 2 fils. Attention soudures difficiles, ne pas utiliser une température de soudure trop élevée.
Mesurer la résistance avec le premier ohmmètre à portée de main :
– Aux bornes des fils
– Aux de résistance supra

Pensez-vous que la mesure de résistance de l’échantillon est significative ?

Biensûr que non ! La résistance à température ambiante est de l’ordre du \( m\Omega \) , probablement loin de la gamme de votre ohmmètre ! De plus en travaillant dans cet ordre de grandeur, les résistances des fils, des soudures, des contacts etc… ne sont plus négligeables.
Il sera impossible de mesure une chute de résistance avec un simple ohmmètre, il nous faut un nouvel appareil de mesure !

A la quête d'un milliohmmètre, kelvin à la rescousse !

Montage 4 fils / Kelvin avec résistance de référence :

Analyser ce circuit, justifier les valeurs de résistance et d’intensité indiquées (ordre de grandeur)
Pont diviseur de tension, retrouver \( R_s = R_e * V_s / V_e \)
Pourquoi ce circuit permet-il de contourner le problème des résistances parasites ?

Il existe d’autres méthodes de mesure pour répondre à notre problème. Celle-ci correspond bien à nos attentes, cependant l’utilisation d’un amplificateur de tension peut être source d’erreur.

Retrouver la résistance de l’échantillon à température ambiante.

Création d'un thermomètre.

Quelle est la température de l’azote liquide (dans les conditions expérimentales) ?

On va utiliser l’azote liquide pour le refroidir l’échantillon, cependant il nous faut un thermomètre pouvant fonctionner à cette température.

La pt100 est connue pour avoir une résistance de 100 \( \Omega \) à \( 0°C \). Comment évolue la résistivité d’un métal conventionnel en fonction de la température ?
Pourquoi la résistance peut-elle faire office de thermomètre ?

Le calibrage du thermomètre demandera une courbe d’étalonnage qui peut être trouvée facilement en ligne…

Bonus : Justifier puis comparer l’approximation linéaire à d’autres modèles (2ème ordre par exemple)

Enfin les mesures !

Apposer la thermomètre sur l’échantillon.
Bricoler un système permettant des variations lentes de température, il est fortement conseillé de refroidir le système à \( 77K \) puis prendre les mesure en laissant le système se réchauffer lentement.

Enfin, vous avez de quoi effectuer la mesure de :

\[ R = f(T) \]

Observer la chute/le saut brutal(e) de résistance et relever \( T_c \)
Vérifier le régime linéaire pour les hautes températures
\[ > 180 K \]

Upgrades

Votre mesure de \( T_c \) correspond-elle aux données constructeurs ?
Quels sont, selon vous, les facteurs limitants de votre expérience ?
Pensez-vous que le thermomètre mesure exactement la température de la résistance supra ?
Quelle est votre vitesse de balayage ? (\( K / min \))

Autant de questions qui soulèvent le défaut principal de la mesure, la thermalisation.

A titre indicatif, une bonne mesure faite en laboratoire se fait à une vitesse moyenne de

\[ 2K/min \]

au voisinage du saut.

La mesure des grandeurs : résistance et température, est difficile à améliorer, mais le ohmmètre et thermomètre improvisés ici sont loin d’être très précis, n’oubliez pas de reporter et calculer les incertitudes.
Cependant vous pouvez facilement améliorer l’isolation du système avec un peu de bricolage.
Soyez créatifs !

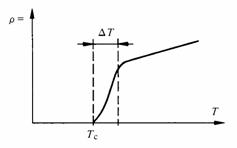
Bonus

Quelle que soit la précision de la mesure, on ne parvient jamais à obtenir une courbe totalement discontinue (prédiction théorique).
La transition supraconductrice s’effectue pendant un petit intervalle de température la notion de \( T_c \) devient ambigüe).
Il faut savoir que la température critique d’un supraconducteur est sensible en sensible par rapport à sa concentration en oxygène.
Pouvez expliquer pourquoi la transition se fait progressivement ?