Il suffit d’attacher la masse à la ficelle et de laisser pendre le tout du toit jusqu’au sol.

Attention, il faut que la masse soit, si possible, sphérique pour limiter les frottements de l’air et se rapprocher d’une masse ponctuelle. Mais aussi quelle soit suffisamment lourde pour rendre le poids de la ficelle négligeable ammenant le baricentre des masses au bonne endroit.

Il faut privilégier une ficelle fine pour là aussi limiter les frottements, du fil de pêche est une bonne solution car il est à la fois très fin et très solide.

Attention aussi à ce que votre point d’accroche soit bien fixe et que le fil ne bouge pas ce qui pourrait entrainer plus de frottement.

Maintenant il faut faire osciller le pendule. Il n’y a pas besoin de faire de grande oscillations, plus l’angle est petit plus l’approximation théorique est juste.

Quand vous lancez la masse, attention à l’éventuelle élasticité de votre ficelle (en particulier si vous avez pris du fil de pêche) !

Ensuite, mesurez (à l’aide du chronomètre de votre smartphone) le temps nécessaire pour faire un certain nombre d’oscillations et d’appliquer la formule précédente.

Pour mesurer les angles, on utilise l’inclinomètre d’un smartphone. Afin de pouvoir correctement viser le sommet de la cible, on utilise un pointeur laser que l’on scotch au téléphone pour être sûr que les deux ont la même inclinaison (le laser doit être assez puissant pour être visible malgré la distance).

On construit une structure en lego modulable pour tenir le smartphone et pouvoir modifier l’angle.

Après avoir mesuré un angle à un point quelconque, on s’éloigne d’une distance que l’on choisit (par exemple 5m, attention il faut le plus précis possible lorsqu’on s’écarte) et on remesure l’angle.

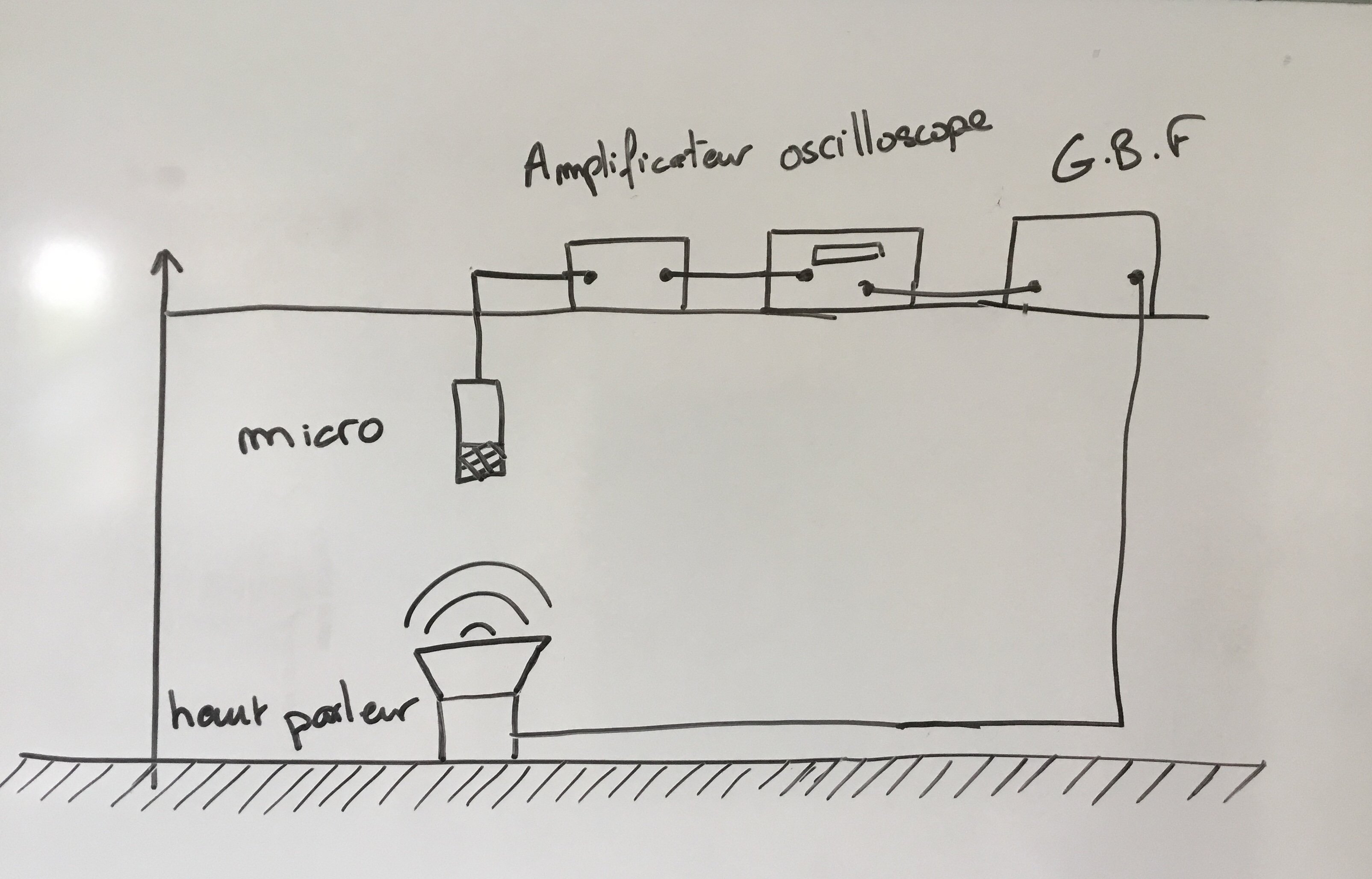
On place un haut-parleur au sol et un micro au niveau du toit.

On envoit un signal sinusoïdal d’une fréquence de l’ordre du kilohertz à l’aide d’un GBF. On réceptionne le signal via le micro, attention celui-ci sera trop faible il faut donc utiliser un amplificateur et on filtre les fréquences pouvant parasiter le signal.

On observe les deux sinusoïdes à l’oscilloscope et on se place à une fréquence pour avoir un déphasage notable (en phase ou en oppostion de phase par exemple) et on cherche la fréquence la plus proche correspondant à un déphasage de ​\( 2\pi \)​ (soit le même déphasage que précédemment).

On utilise la formule

\[ \frac{c}{\nu_1-\nu_2}=L \]

On peut moyenner la différence de fréquences en faisant plusieurs déphasage de ​\( 2\pi \)​.

On peut aussi envoyer un créneau et mesurer la différence de temps entre les fronts montants.

Il faut pour cela, garder le même montage mais se placer en basse fréquence pour que ce temps soit petit devant la période du créneau.